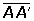¿Qué es el cálculo?
Rama de las matemáticas que se ocupa del estudio de los incrementos en las variables, pendientes de curvas, valores máximo y mínimo de funciones y de la determinación de longitudes, áreas y volúmenes. Su uso es muy extenso, sobre todo en ciencias e ingeniería, siempre que haya cantidades que varíen de forma continua.
El cálculo se divide en dos áreas generales: cálculo diferencial, que se ocupa de encontrar la velocidad de cambio de una función, y el cálculo integral, que utiliza un proceso de límites para obtener gradualmente mejores aproximaciones al valor verdadero. El cálculo integral surgió del problema de tratar de calcular el área dentro de una frontera curva, que no se puede encontrar simplemente utilizando las fórmulas convencionales para calcular las áreas de los polígonos.

El cálculo en la cotidianidad
En mi experiencia personal el cálculo es parte de la vida diaria, ha estado involucrado en la remodelación realizada por mi papá en nuestra vivienda ya que tuvo que calcular todos los materiales y costos a utilizar.
Aplicación del cálculo en ingeniería civil.
El cálculo es básico en la ingeniería civil, ya que es la base de todo, esta implícito en todas las actividades que ejecuta un ingeniero civil desde el cálculo de los cómputos métricos para realizar una actividad, hasta el cálculo matemático que sirve para la elaboración de un proyecto.

jueves, 16 de diciembre de 2010
viernes, 5 de noviembre de 2010
Hipérbola
-La hipérbola posee una excentricidad mayor que uno, la cual se define como la distancia del centro hacia uno de los focos, dividida, la distancia del centro a uno de los vértices.
- La longitud del eje mayor se define como dos veces la distancia del centro hacia cualquiera de los puntos del eje mayor.
-La longitud del eje conjugado se define como dos veces la distancia del centro hacia cualquiera de los puntos del vértice del eje menor.


Paso 2: se resuelven los polinomios.
Paso 3: se resuelve la distributiva.
Paso 4: se iguala la ecuación a 0.
Paso 5: se agrupan los términos semejantes.

- No olvidar la posición de los signos, de a y de b en la ecuacion canonica para no confundir los ejes a los que son paralelas las hipérbolas.
http://www.vitutor.com/geo/coni/hres.html
http://www.cidse.itcr.ac.cr/cursos-linea/SUPERIOR/t1-conicas/4-Hiperbola/index.html
libro: álgebra de baldor.
lunes, 18 de octubre de 2010
Triángulos
Clasificación de los triángulos según la amplitud de sus ángulos: