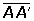Hipérbola

Concepto y definición:

Lugar geométrico: una curva es el lugar geométrico de todo aquello puntos, solamente de aquellos puntos, que satisfacen una o mas condiciones geométricas dadas.

Se llama ecuación de un lugar geométrico plano a una ecuación de la forma f(x,y)=0 cuyas soluciones reales para valores correspondientes de x y y son todas coordenadas de aquellos puntos, y solamente de aquellos puntos que satisfacen la condición o condiciones geométricas dadas que definen lugar geométrico.

Hipérbola: Una hipérbola es el lugar geométrico de los puntos tales que el valor absoluto de la diferencia de sus distancias a dos puntos fijos, llamados focos, es igual a una constante positiva igual a la distancia entre los vértices.

Elementos

Centro: Es el punto de intersección de los ejes.

Distancia focal: Es el segmento de logitud 2c.                             

Eje mayor: Es el segmento 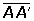 de longitud 2a.

Eje menor: Es el segmentode longitud 2b. 

Vértices: Los puntos A y A' son los puntos de intersección de la hipérbola con el eje focal. Los puntos B y B' se obtienen como intersección del eje imaginario con la circunferencia que tiene por centro uno de los vértices y de radio c.

Focos: son los fijos Fy F.

Eje focal: es la recta que pasa por los focos.

Tipos y características.

Vertical: Si el centro de la hipérbola es C(x0, y0) y el eje principal es paralelo a Xo, la ecuación de la hipérbola será:

   

 eje vertical.

Horizontal: Si el centro de la hipérbola C(x₀, y₀) y el eje principal es paralelo a Yo, la ecuación de la hipérbola será:

eje horizontal

Características
-La hipérbola posee una excentricidad mayor que uno, la cual se define como la distancia del centro hacia uno de los focos, dividida, la distancia del centro a uno de los vértices.
- La longitud del eje mayor se define como dos veces la distancia del centro hacia cualquiera de los puntos del eje mayor.
-La longitud del eje conjugado se define como dos veces la distancia del centro hacia cualquiera de los puntos del vértice del eje menor.

Leyes e identificación.

Leyes

La Ley de Boyle, pv= C, es una relación hipérbola. Esto mismo se puede afirmar de la relación que existe entre dos cantidades. Cualesquiera que sean inversamente proporcionales.

Identificación:

·         Ambas variables están al cuadrado.

·         Esta igualado a uno( =1.)

·         Diferente signo.

Ecuaciones

Ecuación general de la hipérbola:

 

Ecuación canónica de la hipérbola:

  

eje vertical. C(h,k)

 

eje horizontal C(h,k)

  

Procedimiento:

Como se pasa una ecuación general a la canónica:

  (Los coeficientes de los variables al cuadrado debe ser de diferente signos)

Paso 1: Poner el término independiente después de la igualdad.

Paso 2: Agrupamos las variables (x,y)

Paso 3: Sacamos factor común

Paso 4: Completamos al cuadrado

Paso 5: Se suman

Paso 6: Pasamos el termino independiente dividiendo para que quede 1

Paso 7: Pasamos el “A” dividiendo al “Po”

Paso 8: Sacamos m.c.m

Como se pasa una ecuación canónica a la general:

Paso 1: sacamos m.c.m para eliminar el denominador.
Paso 2: se resuelven los polinomios.
Paso 3: se resuelve la distributiva.
Paso 4: se iguala la ecuación a 0.
Paso 5: se agrupan los términos semejantes.

Y obtenemos:        

Gráficas

hipérbole vertical

Hipérbole horizontal 

Ejercicios tipo

Representa gráficamente y determina las coordenadas del centro, de los focos, de los vértices y la excentricidad de las siguientes hipérbolas:

 

Errores comunes  

• No olvidar la posición de los signos, de a y de b en la ecuacion canonica para no confundir los ejes a los que son paralelas las hipérbolas.

Conocimientos

 

Tener presentes conceptos de matemática básica para la resolución de las ecuciones como, factorización, resolución de ecuciones de segundo grado, suma y resta de fracciones y muy importante despejes.

LINKS 

http://www.vitutor.com/geo/coni/h_1.html
http://www.vitutor.com/geo/coni/hres.html
http://www.cidse.itcr.ac.cr/cursos-linea/SUPERIOR/t1-conicas/4-Hiperbola/index.html
libro: álgebra de baldor.